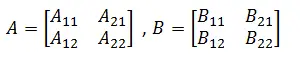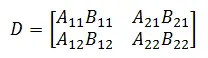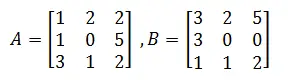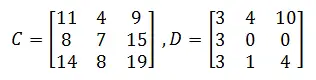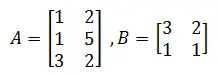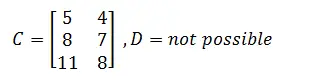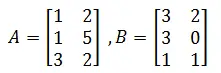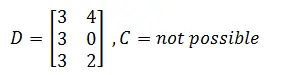Matrix Multiplication – Matlab

Matrix multiplication is likely to be a source of a headache when you fail to grasp conditions and motives behind them. Here, we will talk about two types of matrix multiplication and how you can handle them both manually and using Matlab.

One of the best ways to test your understanding of the following is to work them out manually and then using Matlab to check your result.

Matrix multiplication theory reminder

Let’s consider the following matrices.

Matrix product

Here is the formula for multiplying the above matrices, and I will highly recommend you check the properties of Matrix multiplication and most importantly the dimension agreement that is crucial between two matrices that need to be part of a multiplication.

Generally speaking, if A is an n × m matrix and B is an m × p matrix, their matrix product AB is an n × p matrix, in which the m elements across the rows of A are multiplied with the m elements down the columns of B

Matrix multiplication element by element

In the other side, we have the element by element matrix multiplication, which is rather a straightforward operation, here is the formula used.

It is simply the product of matrices, element by element, this type works only when the dimensions of the matrices are equal. To be more specific, if A is an n × m matrix, B has to be an n × m matrix for this to work.

Matlab Matrix Multiplication

The following code allows finding a matrix product in Matlab

C=A*B

and this one is the code to find the product of matrices, element by element

C=A.*B

Matrix multiplication examples

Example 1

If we keep the same logic as above while varying the value of A and B, but knowing that C is the matrix product and D is the element by element matrix multiplication.

Matlab code

A=[1 2 2; 1 0 5; 3 1 2];
B=[3 2 5;3 0 0; 1 1 2];
C=A*B
D=A.*B

Results

Example 2

Matlab code

A=[1 2;1 5;3 2];
B=[3 2;1 1];
C=A*B

Results

Example 3

Matlab code

A=[1 2;1 5;3 2];
B=[3 2;3 0; 1 1];
D=A.*B

Results