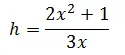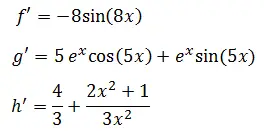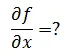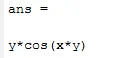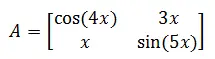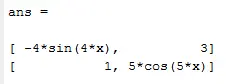Derivative in Matlab

In this post, we will pay some attention to one of the basic operations of calculus which is Derivation.

We are not going to go into Derivative formulas here. We will right dive into helping those who need to find a derivative jump into Matlab and quickly get what they are looking for, without having to do it manually.

Matlab has a set of inbuilt functions that deal with such operations.

Content

Derivative in Matlab
Derivation of a constand in Matlab
Second derivative in Matlab
Partial derivative in Matlab
Derivative of a matrix in Matlab

Derivative in Matlab

Let’s consider the following examples

Example 1

Example 2

Example 3

To find the derivatives of f, g and h in Matlab using the syms function, here is how the code will look like

syms x
f = cos(8*x)
g = sin(5*x)*exp(x)
h =(2*x^2+1)/(3*x)
diff(f)
diff(g)
diff(h)

Which returns the following (You can decide to run one diff at a time, to prevent the confusion of having all answers displayed all at the same time)

Where we can depict the following

Derivative of a constant

We know that the derivative of any constant term is null but if for some reasons you want to find the derivative of a constant using Matlab, here is how you need to proceed.

constant = sym('5');
diff(constant)

Second derivative in Matlab

To find the second derivative in Matlab, use the following code

diff(f,2)

or

diff(diff(f))

Both will give the same result.

Partial derivative in Matlab

To find the derivative of an expression containing more than one variable, you must specify the variable that you want to differentiate with respect to. The diff function will help calculates the partial derivative of the expression
with respect to that variable.

 Example

What is the partial derivative of f with respect to x?

Here is how to do it in Matlab

The code

syms x y
f = sin(x*y)
diff(f,x)

which returns

Derivative of a Matrix in Matlab

You can use the same technique to find the derivative of a matrix.

If we have a matrix A having the following values

The code

syms x
A = [cos(4*x) 3*x ; x sin(5*x)]
diff(A)

which will return